Berechnung einer Armkugel mit dem Satz des Pythagoras

Als erstes braucht es einen Armausschnitt: Den mache ich immer so zwischen 20 und 22 cm hoch. Bei größeren Größen können es auch 25 cm sein, bei Männergrößen auch 30 cm. (Weil ich auch immer eine Schulterschräge (2 cm) mache, ergeben sich vom unteren Rand des Armausschnittes 22-24 cm bis zur obersten Kante). Die Tiefe des Ausschnitts berechnet sich, indem ich meine Schulterbreite messe. Dies mache ich an der äußeren Kante des spitzen Knochens, der da oben aus der Schulter ragt {Emotic(wink2)}, bei mir sind es beispielsweise 36 cm. Ein Vorder- oder Rückenteil ist bei mir 45-47 cm breit, also nehme ich an beiden Seiten je 4,5-5,5 cm weg. Meist sind das 10-12 Maschen, die dann folgendermaßen abzuketten sind. In jeder 2. Reihe 1x3, 2x2, 3x1 (und in jeder 4. Reihe noch 2x1) Maschen. Fertig ist der Armausschnitt.

Wenn das Vorder- und das Rückenteil fertig sind, kann man die Armkugel berechnen. Zunächst geht es um den Schnitt in cm. Dafür misst man die Länge der Kante des Armausschnittes, so wie in der Zeichnung, und nennt diesen Wert c.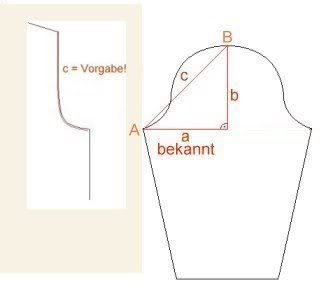

[Beispiel: Ich habe bei meinem Pulli 25 cm Kantenlänge gemessen]

Außerdem sollte schon bekannt sein, wie breit der Ärmel kurz vor Beginn der Armkugel ist. Die Hälfte dieser Breite bekommt den Namen a.
[Im Beispiel waren das 19 cm, die Hälfte von 38 cm.]

Jetzt muss man den Satz des Pythagoras benutzen, der für jedes rechtwinkelige Dreieck gilt.
a²+b² = c².
a und c sind bekannt. b interessiert uns, die Höhe der Armkugel.
Durch Umformen
b² = c²-a²
und Wurzelziehen
b = √( c²-a²)
bekommt man die Formel, in die man die Zahlen einsetzen kann.
[Im Beispiel bekommt man für das unbekannte b = √( 25²-19²) = √( 625-361) = √264 = 16,248..., also 16 cm. Die Armkugel soll also 16 cm hoch werden.]


Nun muss man anhand der Maschenprobe berechnen, wie viele Reihen das werden.
[Im Beispiel ergaben sich bei einer Maschenprobe von 23 Maschen x 30 Reihen → 48 Reihen.]

Weil man in jeder 2. Reihe abnimmt, stehen dann halb so viele Abnahmen wie Reihen zur Verfügung, um die Kurve zu formen. Diese Kurve soll – wie in der Zeichnung – die Eigenschaft haben, dass sie sanft ansteigt, immer steiler wird und dann langsam wieder flach wird. Das heißt, man muss mehr, dann weniger, dann immer weniger, dann wieder mehr und mehr Maschen jede zweite Reihe abketten.
Außerdem sollte man am Ende eine gewisse Anzahl Maschen auf einmal abketten und den Ärmel damit beenden. Meiner Erfahrung nach sind das 8-12 Maschen bei Nadelstärke 3-4, natürlich mehr oder weniger je nach Nadelstärke und daraus resultierender Maschenzahl. Als Faustregel kann man beispielsweise 14% nehmen.

[In meinem Beispiel habe ich zu Beginn der Armkugel 84 Maschen, 14% davon sind 12 Maschen.]

Die Differenz aus der Maschenzahl am Anfang und den (beispielsweise) 12 am Ende muss man abnehmen. Weil die Abnahmen symmetrisch sind, [Im Beispiel: 84-12 Maschen = 72 Maschen, also pro Seite je 36 Maschen. Diese Maschen müssen nun in 48 Reihen abgenommen werden.]

Nun folgt reine Empirie. Ich beginne meist mit 1x4 Maschen abketten und mehrmals 2 Maschen, dann eine Weile nur eine Masche, dann wieder mehrmals 2 Maschen, am Ende 4 Maschen.
[Dies ergab folgende Anleitung: Abnehmen in jeder 2. Reihe: 1x4, 3x2, 16x1, 3x2, 1x4 Maschen, dann die letzten 12 Maschen. Also 36 Maschen in 48 Reihen abgenommen. ]
Voilà!

Aber Achtung! Wenn man sehr dünne Nadeln verwendet, kann die Armkugel schon mal sehr viele Reihen hoch werden, so dass man in der Mitte der Abnahmen dazu übergehen muss, jede 4. Reihe eine Masche abzuketten. Auch wenn man Wert auf sehr gut passende Ärmel legt, werden die Armkugeln sehr steil.

Wie man auf der Zeichnung weiter oben sehen kann, ergibt das "wellige" Abnehmen automatisch eine längere Strecke als das vorher gemessene c. Also die geschwungene Linie zwischen A und B ist etwas länger.
[Bei mir waren das statt 25 cm ganze 30 cm]

Das ist aber genau richtig und gut, denn man näht solche Ärmel im oberen Drittel etwas "eingehalten" ein, so dass die Kugel tatsächlich etwas kugelig wird.

Viel Spaß!


August 2010

Der Anti-Pythagoras

Endlich! Lange erwartet, jetzt erhältlich.
Ich hatte mich mit meinem Pythagoras verkünstelt, aber ich bin reumütig und mache das gut. Denn das, was man mit komplizierten Additions- und Wurzelzieh-Manövern bekommt, lässt sich auch ohne viel Worte in einem einzigen Bild darstellen:

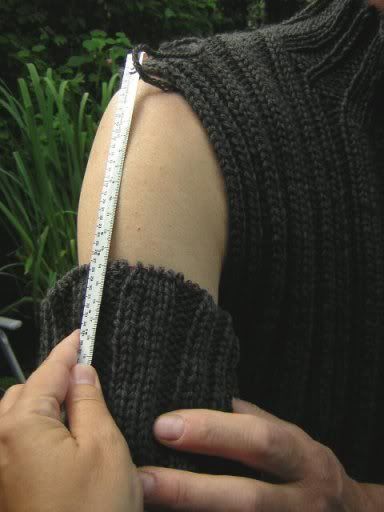
Man bekommt den Abstand ab Beginn der Armkugel bis oben. Hier sind es zum Beispiel 13 cm. Das kann man auch einfach abmessen und dank der Elastizität der Strickerei passt das dann schon. Wichtig ist, dass man sich die Ränder an der unteren Kante des Armausschnitts fixiert denkt (oder mal schnell mit Sicherheitsnadeln fixiert), damit auch die Ärmellänge am Handgelenk in Ordnung ist.

Komplizierter ist eigentlich die Kurve der Abnahmen, die nun notwendig ist. Das ist das eigentliche Problem.
Hier habe ich zum Beispiel 88 Maschen und will am Ende - sagen wir - 12 übrig haben. Nun muss ich die erforderliche Reihenzahl für die fehlenden 13 cm ermitteln und die Abnahmen für die Armkugel schön staffeln, zum Beispiel noch 44 Reihen, dann muss ich 1x4, 1x3, 3x2, 12x1, 3x2, 1x3, 1x4 und die restlichen 12 Maschen abketten.
So!